Buffers

The acidity of the internal environment in the human body is maintained within a very narrow range of pH values. This is because the properties of proteins and other molecules depend on pH. If there is a significant change in pH, for example, the speed of enzyme reactions, the properties of receptors, transporters and ion channels, etc. will change significantly. It is both the effect of substances that we take in as food or with which our skin comes into contact, as well as the production of acids and bases through metabolic processes.

Buffers (also buffers, buffer solutions, resistant solutions) are involved in maintaining the pH of the environment .

In most textbooks, a buffer is defined as a conjugated pair of acid (or base) that is able to maintain a stable pH within a certain range even after adding a strong acid or base to the system. By conjugate pair we mean an acid (or base) and its salt, which is formed after adding a base (or acid) to the system. It is a pair of substances that change into each other through the gain/loss of one proton. If it is a strong acid (or base), it is (almost) completely dissociated, and thus all available particles will participate in any reaction (e.g. HCl-KCl buffer, dissociated into H + , Cl - and K + ). Far more often, weak acids are used, whose undissociated parts (e.g. CH 3COOH) represent a storage pool, the splitting of which (into CH 3 COO - and H + ) will occur after the addition of a substance with a different pH.

The exact calculation of theoretical pH is very complicated (temperature, concentration of individual buffer components, activity coefficients, solvent, ionic strength of the system, etc. must be taken into account). Therefore, more often the pH of systems is measured experimentally. The simplest estimate of buffer pH is the Henderson-Hasselbalch equation (hereinafter referred to as H.-H. rce ). It can be derived by logarithmizing equation (1) for the equilibrium constant:

$K_{a}={\frac {[{\mbox{H}}^{+}]\cdot [{\mbox{A}}^{-}]}{[{\mbox{HA}}]}}$, resp. $K_{b}={\frac {[{\mbox{B}}^{+}]\cdot [{\mbox{OH}}^{-}]}{[{\mbox{BOH}}]}}$,

where HA (or BOH) represents the acid (base), A - (B + ) the anion of the acid (or the cation of the base), and the square brackets are the molar concentration. The given equation is inaccurate, because instead of concentrations, activity must be taken into account. For the acid and its salt, the simplified equation (2) applies:

(2)

$pH=pK_{a}+\log {\frac {[{\mbox{A}}^{-}]}{[{\mbox{HA}}]}}$;

similarly for the base and its salt equation (3):

(3)

$pOH=pK_{b}+\log {\frac {[{\mbox{B}}^{+}]}{[{\mbox{BOH}}]}}$,so $pH=14-pK_{b}-\log {\frac {[{\mbox{B}}^{+}]}{[{\mbox{BOH}}]}}$.

The composition of the buffers is more or less complicated and depends primarily on the purposes for which the chosen system is to be used. The optimal activity area of ​​the selected buffer is determined by its composition. Among the simpler ones, we can mention the Clark–Lube buffer (HCl+KCl) pH 1.1–2.2; citrate pH 2.2–3.6; phosphate (NaH 2 PO 4 + Na 2 HPO 4 , used for blood pH range) – pH 5.8–8.0. However, multi-component buffers exist and are also used, the effective range of which covers practically the entire pH range, e.g. Britton's–Robinson's, whose effective range of activity ranges from pH 1.8 to almost 12.

The number of moles of monoacid and salt in the buffer and the amount of monoacid added to the buffer can be calculated according to equations (4):

(4)

$n_{{\text{s}}^{\circ }\!\!\!{\text{ul}}}=[{\mbox{A}}^{-}]\cdot V_{\text{buffer}}$;     $n_{\text{acid}}=[{\mbox{HA}}]\cdot V_{\text{buffer}}$;     $n_{{\text{p}}{\check {\text{r}}}{\acute {\iota }}{\text{davek}}}=[{\mbox{H}}^{+}]\cdot V_{{\text{p}}{\check {\text{r}}}{\acute {\iota }}{\text{davek}}}$

To calculate the theoretical pH value of buffers consisting of a weak acid and its salt after the addition of acid, the relation (5a) derived from H.-H. rce (2).

(5a)

$pH=pK_{a}+\log {\frac {n_{{\text{s}}^{\circ }\!\!\!{\text{ul}}}-n_{{\text{p}}{\check {\text{r}}}{\acute {\iota }}{\text{davek}}}}{n_{\text{acid}}+n_{{\text{p}}{\check {\text{r}}}{\acute {\iota }}{\text{davek}}}}}$

and after adding the principle to the same system then equation (5b): |}

$pH=pK_{a}+\log {\frac {n_{{\text{s}}^{\circ }\!\!\!{\text{ul}}}+n_{{\text{p}}{\check {\text{r}}}{\acute {\iota }}{\text{davek}}}}{n_{\text{acid}}-n_{{\text{p}}{\check {\text{r}}}{\acute {\iota }}{\text{davek}}}}}$

where the index "buffer" refers to the volumes before the addition of acid (or base), "salt" to the salt contained in the buffer, "acid" to the acid in the buffer and "addition" only to the values ​​of the addition itself before mixing with the buffer.

An analogous relationship derived from equation (3) is used for a weak base and its salt.

The simplest calculations can be performed for uni-univalent systems, i.e. on the assumption that the buffer consists of a monovalent weak acid and its salt (e.g. CH 3 COOH/CH 3 COONa, NaH 2 PO 4 /Na 2 HPO 4 ) and is added also a monobasic base or acid (e.g. HCl or NaOH).

The theoretical pH value of the buffer often differs from the experimentally determined one (whether due to non-idealities or intentionally neglected factors during their calculation (ionic strength, temperature, solvent, etc.)). Therefore, buffers are often prepared in two stages: first, the components are mixed in a calculated (tabulated) ratio so that the result corresponds to the desired pH value, then its actual pH value is measured using a properly calibrated pH meter, and a sufficiently accurate value is achieved by the appropriate addition of acid or base (after each addition, the system must be properly mixed, let the temperature equalize and read the value of the device only after stabilization).

The amount of a substance, the addition of which can be compensated with the help of a buffer, is determined by the so-called buffering capacity β . It is mainly determined by the composition and concentration of the buffer. The higher the concentration of the buffer components, the higher the buffering capacity (e.g. for a narrow range of buffers and small expected additions of substances, a low-concentration buffer can be used and vice versa). Buffering capacity decreases with buffer dilution. Buffers composed of weak acids and their salts (or weak bases and their salts) with the same substance concentration, i.e., more precisely, for which pH = pK, have the largest capacity. This can be derived from equation (2) and (3), where with equal concentrations of the acid salt (resp. base) log(1/1) = 0 and pH = pKa (resp. pH = 14 − pK b). At other ratios, it changes according to the logarithm of the ratio of the concentrations of the individual components. In general, the literature states that a "simple" buffer, composed of two components, is usable in the pH range from (pK a − 1) to (pK a + 1) (i.e., the ratio of acid to salt ranges from 10:1 after 1:10).

A simplified, empirical calculation of the buffering capacity β is performed according to the following equation (6):

$\beta ={\frac {dc_{b}}{dpH}}\approx {\frac {\Delta c_{b}}{\Delta pH}}=-{\frac {\Delta c_{a}}{\Delta pH}}$,

where "d" denotes the derivative (read "dé cé according to dé péHá"), Δc a change in the molar concentration of the acid, Δc b the change in the molar concentration of the base, ΔpH the change in pH achieved by the addition of acid Δc a or base Δc b .

A more accurate relationship enabling the calculation of β is obtained by differential modification of H.-H. rce

(7a)

$\beta =2,3\cdot \left([{\mbox{H}}^{+}]+[{\mbox{OH}}^{-}]+{\frac {K_{a}\cdot c_{a}\cdot [{\mbox{H}}^{+}]}{([{\mbox{H}}^{+}]+K_{a})^{2}}}\right)\approx 2,3\cdot c_{a}\cdot {\frac {K_{a}\cdot [{\mbox{H}}^{+}]}{(K_{a}+[{\mbox{H}}^{+}])^{2}}}=2,3\cdot [{\mbox{A}}^{-}]\cdot \left(1-{\frac {[{\mbox{A}}^{-}]}{c_{a}}}\right)$

where c a denotes the total concentration of the buffer (the sum of the molar concentrations of the buffer components), i.e. ca = [HA] + [A - ], and K a the dissociation constant (acidic component) of the buffer system (the constant 2.3 is approximate and ensures the conversion natural and decimal logarithms).

An analogous equation (7b) applies to the buffering capacity of mixtures of weak bases and conjugated acids:

(7b)

$\beta =2,3\cdot \left([{\mbox{H}}^{+}]+[{\mbox{OH}}^{-}]+{\frac {K_{b}\cdot c_{b}\cdot [{\mbox{OH}}^{-}]}{([{\mbox{OH}}^{-}]+K_{b})^{2}}}\right)\approx 2,3\cdot c_{b}\cdot {\frac {K_{b}\cdot [{\mbox{OH}}^{-}]}{(K_{b}+[{\mbox{OH}}^{-}])^{2}}}$

The first part of the equation also includes the buffering capacity of strong electrolytes (strong acids and strong bases), while a simplified formula is used for the approximate calculation of the buffering capacity of buffers created from weak acids of the HA type. To calculate the buffering capacity, relation (7c) is also often used, which is created by a simple modification of relation (7a):

(7c)

$\beta =2,3\cdot [{\mbox{A}}^{-}]\cdot \left(1-{\frac {[{\mbox{A}}^{-}]}{c_{a}}}\right)$

Buffer preparation

The preparation of buffers is based either on solutions of weak acids or bases and their salts, or from solid salts of polyhydric acids or their solutions, or a weak acid is partially neutralized, or base with a strong base, or acid.

If we prepare the buffer exactly according to the instructions and measure its pH, the pH may not always correspond exactly to the theoretically calculated value. Especially in more concentrated solutions, the activity of hydrogen ions tends to be lower than their concentration. The weights of individual components for the preparation of the most common buffers can be found in the tables.

Acetate buffer titration

titration curve

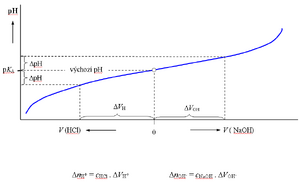
The graphical representation of the Henderson-Hasselbach equation is the titration curve of a weak acid or base. When titrating the buffer , i.e. when dilute solutions of a strong acid or base are gradually added to the buffer solution, the pH initially changes only slowly, after exceeding the value of pH = KA ± 1, the changes are already significant. The buffering capacity for any pH value can be determined from the course of the titration curve of the buffer of a given concentration ( cHB + cnB ).

By mixing equal volumes of solutions of acetic acid and sodium acetate with the same substance concentration, a buffer with a ratio of components of 1:1 is created, the pH of which is equal to the pKA of acetic acid (4.75).