Flick's laws
{{Was checked | 20141214063925 | Carmeljcaruana
|
Check of this article is requested. Suggested reviewer: Carmeljcaruana |
Flick's Law[edit | edit source]
Fick's Law, discovered by Adolf Fick, is a common used principle when looking at Diffusion whether it is determining the rate of diffusion or the result of the concentration of particle in a substance. The equations founded by Fick is applied to modern pharmaceuticals, models for understanding transport processed, bio-polymers etc...
Fick’s First Law[edit | edit source]
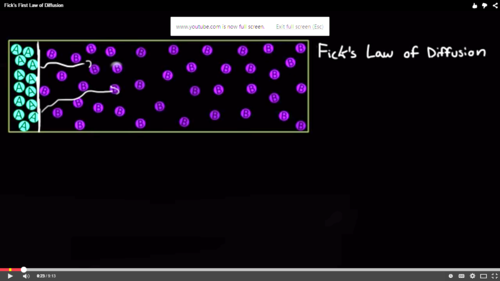
[1] Fick’s First Law shows how much flux to expect in a system under steady states. It describes the fundamental laws of diffusion where particles which he refers to as Flux goes from regions of high concentration to regions of low concentration with a magnitude that is proportionate to the concentration gradient. Adolf Fick was able to deduce this law by measuring the number of Particle, A crossing a set area per time giving: (Amount of A particles )/(Area ×Time) . This he referred to as flux also is known as J(Ax).
Where ‘A’ is the particle and ‘x’ is the direction that the particle travels. This gave the equation where the negative diffusion coefficient or diffusivity of particles A and B, '-DAB', is multiplied by the change in concentration of particle A, ‘dCA’, per change in the ‘x’ direction, 'dx'.
J(Ax )=-DAB×(dCA/dx)
Or known as
J(Ax )=-DAB×(∆C/∆x)
∆x=x2-x1 Which would always give a positive number as particle move from regions of high concentration to regions of low concentration
∆C=C2-C2 as Particle A is going from a high/ large concentration to a low/low concentration giving a negative number
DAB, the diffusion coefficient is the speed of how fast a particle diffuses unique to the particles involved e.g. the diffusion coefficient of oxygen onto Nitrogen would be different to the diffusion coefficient of Oxygen into Carbon Dioxide. This is because what particle A diffuses onto, i.e. the properties of Particle B could increase or decrease the Diffusion coefficient.
Using the units…
D=(Area (cm^2))/time(s) ∆C=(Mole (mol))/(Volume (cm^3 ) ) ∆x=length (cm)
we can prove..
mol/cm^3 ×1/cm=mol/cm^4
mol/cm^4 ×cm^2/s=mol/(cm^2×s)=molcm^(-2) s^(-1)
mol/(cm^2×s)=(amount of Particle)/(Area×time) ∴FLUX
As the diffusion coefficient or diffusivity of particles differ depending on what particle A diffuses into, therefore different chemical and physical factors must create and effect on the value of 'D'.
'D' is said to be proportional to the squared velocity of the particles it is also dependant on the tempreture of the system as increase in temperatire increase kinetic activity of particles therefore increasing rate of diffusion. The Viscosity of fluid and size of particles also cause an affect on the value of the Diffusion coefficient.
Fick’s Second Law[edit | edit source]
[2][3][4] Ficks Second Law describes the rate of change, either increase or decrease of concentration in a volume as proportionate to the curvature of the Concentration gradient. This formal is given as ∆C/∆t=D_(∆x^2)/(∆^2 C)Where the increase (or decrease) in concentration over time ∆C/∆t (cm-3 s-1) is proportionate to the Diffusivity, D (cm2), and the curvature which is the second derivative of the first Law ∆C/∆x, giving (∆^2 C)/∆x^2 . As they are proportionate, when the accumulation is positive, the curvature is positive.
Bib
http://www.wikilectures.eu/index.php?title=Flick%27s_laws&action=edit&redlink=1