What drives our cells

Thermodynamics

Chemical reactions

[ ✎ edit embedded article ]

Chemical reactions are events in which one group of compounds, reactants', are transformed into other compounds, products. We describe reactions with chemical equations.

E.g. in the equation

(1)

a A + b B → c C + d D

means

A, B	reactants,
C, D	products,
a, b, c, d	stoichiometric coefficients which express the ratio of the number of particles of the compounds participating in the reaction.

The term "equation" implies the existence of equality between the two sides: in every chemical reaction, mass, energy, and electric charge must be conserved.

Let us now look at the reactions between copper and ferric ions in solution:

(2)

Cu⁺ + Fe³⁺ $\rightleftharpoons$ Cu²⁺ + Fe²⁺

Like most reactions in chemistry (and almost all in biochemistry), this reaction is reversible. It means it can go both ways. The process stops after a certain amount of iron is reduced and a certain amount of copper is oxidized. We say that at this point the reaction has reached an equilibrium state, i.e. that the concentration of reactants and products in the reaction system does not change any further.

The established equilibrium can be mathematically described using the equilibrium constant, K_eq, which is defined as the quotient of the product of the equilibrium concentrations of products and reactants (squared by their stoichiometric coefficients):

(3)

$K={\frac {[C]^{c}\cdot [D]^{d}}{[A]^{a}\cdot [B]^{b}}}$

In the case of reaction (2), we therefore get

(4)

$K={\frac {[Cu^{2+}]\cdot [Fe^{2+}]}{[Cu^{+}]\cdot [Fe^{3+}]}}$

Assume that the equilibrium constant for reaction (1) is equal to 1, i.e. that in the equilibrium state the product of the concentrations of products and reactants is the same. If we now add more compound A to the system, we will break the established equilibrium, and the reaction will therefore start in a direction that will try to restore the original state again. In our case, substance A will react with substance B to form substances C and D as long as the products of concentrations ([A]·[B] and [C]·[D]) are not equal again and a new equilibrium state is reached. This rule is called Le Chatelier's principle.

A system in equilibrium reacts to a change in conditions (pressure, temperature, concentration) in such a way as to suppress this change.

Chemical Potential

[ ✎ edit embedded article ]

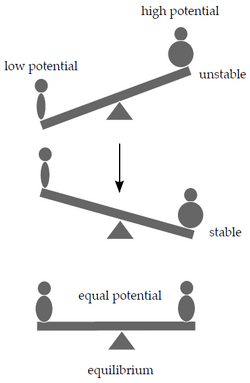
Let's try to get closer to why chemical reactions take place as a response to changes in the system. A swing analogy will help. A heavy person will sooner or later outweigh a lighter one, while two people of the same weight will end up in a state of equilibrium at the same level above the ground after a while.

Chemical potential scheme

We can explain the phenomenon using the potential energy of both people in the Earth's gravitational field. Gravitational potential energy depends on the mass and position of the object in the gravitational field. The system we used in the swing example will try to minimize its potential energy by moving the heavier person as low to the ground as possible.

Similarly, chemical potential μcan be defined as the potential energy contained in a certain amount of substance that can be released during chemical reactions. Analogous to our example with the see-saw, on both sides of the chemical equation are substances with different potentials. If the sum of the chemical potentials of the reactants exceeds that of the products, the reaction will proceed from left to right, and vice versa. If the potentials are equal, the system has reached equilibrium. </noinclude>

Gibbs energy

[ ✎ edit embedded article ]

The difference in chemical potentials of products and reactants is related to a thermodynamic function called change in Gibbs energy (ΔG). Of the many possible definitions of Gibbs energy, two are important for biochemistry:

1. The change in Gibbs energy is equal to the maximum amount of (non-volumetric) work the system can do;
2. The change in Gibbs energy is a measure of the deviation from the equilibrium state.

The first definition tells us that we can use ΔG to predict whether a reaction will occur and whether it can be used as a source of energy for other processes (muscle contraction, movement of ions across a membrane).

The second definition expresses two facts:

a) in equilibrium state, ΔG is equal to zero;

b) changing the concentrations of substances in a system that is not in equilibrium will change (increase or decrease) ΔG.

The meaning of the Gibbs energy change can also be illustrated by the following representation:

If a reaction starts with only a mixture of reactants, it will proceed towards products as long as 'ΔG is negative. If the chemical potential of the products becomes the same as that of the reactants, the system has reached the lowest energy state and the reaction stops. The reaction mixture is now at equilibrium. It cannot be assumed that the reaction would continue because ΔG is positive in the next part of the curve.

It therefore applies:

ΔG < 0 – the reaction takes place spontaneously;

ΔG = 0 – 'equilibrium state;

ΔG > 0 – the reaction does not take place spontaneously.

We can also define the change in Gibbs energy through thermodynamic quantities such as enthalpy (H) and entropy (S):

(5)

ΔG = ΔH – T · ΔS

Enthalpy change is the energy released or consumed during a reaction (a negative value means energy is released and vice versa).

Entropy' is often considered to be a measure of the disorder of a system. According to the second law of thermodynamics, disorder (and thus entropy) of all closed systems increases.

It follows from equation (5) that a chemical reaction can be driven (i.e. achieve a negative ΔG) either by a suitable (i.e. negative) change in enthalpy, or by a sufficient increase in entropy, or both at the same time.

For practical reasons, it is convenient to define standard conditions under which ΔG and other quantities are measured, and then use them for calculations under real situations. In chemistry, a pressure of 101,325 Pa, a temperature of 25 °C (298.15 K) and a unit activity (simplified, i.e. one molar concentration of all substances) are considered standard conditions. The quantities that we will measure in these conditions are denoted by index ⁰. Biochemists define their standard conditions at neutral pH, standard quantities are then marked with a comma: ′.

From the table values of ΔG⁰ or ΔG⁰′ we can calculate ΔG for any reaction using the equation:

(6)

$\Delta G=\Delta G^{0}+R\cdot T\cdot ln{\frac {[C]^{c}\cdot [D]^{d}}{[A]^{a}\cdot [B]^{b}}}$

At equilibrium, ΔG is equal to zero and the expression  ${\frac {[C]^{c}\cdot [D]^{d}}{[A]^{a}\cdot [B]^{b}}}$  is equal to the equilibrium constant K_eq.

Thus, equation (6) in the equilibrium state takes the form:

(7)

ΔG = −R · T · ln K_eq

Through this equation, we can then calculate the equilibrium constant from ΔG or vice versa.

The easy availability of ΔG⁰ values can lead to hasty conclusions about the impossibility of the reaction progress when finding positive ΔG⁰ values in the tables. But this should be avoided.

Let's show it with the following example: The metabolic pathway of glycolysis includes a step in which glucose-6-phosphate is converted to its isomer, fructose-6-phosphate. ΔG0' of this reaction is +1.7 kJ/mol. So does this mean that our cells are breaking the laws of thermodynamics by carrying out this reaction every second of our lives?

It is important to keep in mind the difference between ΔG' and ΔG⁰ and ΔG⁰. Only ΔG alone can tell us something about the thermodynamic profile of a particular reaction. The values of ΔG⁰ and ΔG⁰' are valid only when maintaining standard conditions, which are very rarely (if ever) present in nature. In order to assess the probability that a reaction will occur, we need to know the true concentrations of all the substances involved in it.

In our case, enzymes constantly remove fructose-6-phosphate by their action, so its concentration is kept low. The total ΔG of the isomerization of Glc-6-P to Fru-6-P is therefore ``negative (−2.5 kJ/mol) under the conditions found in the cell. So we see that some energetically relatively unfavorable reactions can also take place if they are combined with energetically favorable reactions (in this case, those that drain products or supply reactants).

If the transformation reaction A → B reaches an equilibrium state with a low concentration of substance B, we can combine it with the transformation reaction B → C, which, on the other hand, reaches an equilibrium state only at low concentrations of reactant B. The second reaction then effectively removes the substance B formed by the first reaction and thus prevents it from reaching a state of equilibrium.

In our example of glycolysis, the enzyme phosphofructokinase very efficiently phosphorylates Fru-6-P to fructose-1,6-bisphosphate, thereby preventing the accumulation of Fru-6-P that would inhibit the previous reaction.

Electrochemical equilibrium

[ ✎ edit embedded article ]

Chemical reactions in which the oxidation numbers of elements change are called redox reactions. During oxidation, the oxidation number increases, during reduction, it decreases. These changes usually involve the transfer of electrons from one atom or molecule to another.

If we immerse a zinc rod in a solution of zinc sulfate, a reaction is triggered in which the metallic zinc gives up two electrons and changes to Zn²⁺ until equilibrium is restored. The process leads to the accumulation of electrical charge, which we refer to as electrode potential (E). This can be measured indirectly, as a difference to another potential. We call the potential difference voltage and measure it in volts (V).

To overcome the problem of measuring absolute potential, chemists devised a little trick: they chose one of the electrodes and decided that its potential was considered zero. It is a so-called standard hydrogen electrode. Even the electrode potential is actually a potential difference (and is sometimes referred to as ΔE).

The amount of electric charge (also the value of the electrode potential) is related to the equilibrium constant of the reaction. Recall that ΔG corresponds to the maximum amount of work the system can do. In an electric field, work is done by moving charge across a potential difference (much like mechanical work is done by moving matter in a gravitational field). The relationship between ΔG and E is then expressed by the equation:

(8)

ΔG = −n · F · E

where n is the number of electrons transferred in the redox reaction, F is Faraday's constant (equal to the charge of 1 mole of electrons, approximately 9.648 530 9 · 10⁴ C · mol ⁻¹), E denotes the total potential difference between the two half-reactions.

For the standard electrode potential, we can derive the relation similarly:

(9)

$\Delta E^{0}={\frac {R\cdot T}{n\cdot F}}\cdot lnK$

Outside of standard conditions, this so-called Nernst equation (9) has the form:

(10)

$E={\frac {R\cdot T}{n\cdot F}}\cdot ln{\frac {[reduced{\acute {e}}]}{[oxidized{\acute {e}}]}}$

How can these equations be used to predict whether or not a certain redox reaction will occur? The decisive value is again represented by the ΔG value of the respective reaction. It can be calculated from equation (8).

Consider the reaction:

(11)

Zn + Cu²⁺ $\rightleftharpoons$ Zn²⁺ + Cu

The two half-reactions that take place are:

(12)

Zn $\rightleftharpoons$ Zn²⁺ + 2 e⁻

(13)

Cu²⁺ + 2 e⁻ $\rightleftharpoons$ Cu

Zinc is oxidized while copper is reduced. Standard electrode potentials are usually given in tables as reductions, so the E⁰ value for zinc oxidation must be multiplied by −1. Both half-reactions together form the total reaction potential. In this case, E⁰Zn/Zn²⁺ = +0.76 V (after sign reversal) and E⁰Cu ²⁺/Cu = +0.34 V. The total potential difference is therefore +1.1 V. For reaction (11) occurring under standard conditions, the total potential difference is positive, which means that ΔG (in our case ΔG⁰) is negative and the reaction will proceed spontaneously. Under non-standard conditions, we must use the full Nernst equation for both half-reactions.

Kinetics

[ ✎ edit embedded article ]

Kinetics deals with 'what rate and whether a particular reaction will take place.

File:Activation-energy-without-enzyme-cj.png

There are many thermodynamically favorable reactions that do not occur spontaneously.

Everyone knows that burning wood in the air releases a large amount of energy that can be turned into work. Oxidation of wood cellulose by oxygen to water and carbon dioxide must have negative ΔG values. How is it that there are any forests left in our oxygen-rich atmosphere? Similarly, diamonds, often considered "eternal", are thermodynamically unstable modifications of graphite or carbon black.

Some reactions may be thermodynamically feasible, but kinetically improbable.' This phenomenon, called a kinetic barrier, is caused by the existence of unstable transition states (activated complexes). These are formed only when a larger amount of energy is supplied (the formation of an activated complex is thermodynamically unfavorable). This additional energy is called activation energy' (E_A).

Reaction speed

[ ✎ edit embedded article ]

chemical kinetics deals with the study of reaction rate.

In order for two or more substances to react, their molecules must "collide". The probability of a collision increases with increasing temperature, pressure, and concentration of substances.

"Reaction rate (v)" can be defined as the rate of "decrease of reactants" or the rate of "increase of products", i.e. for the reaction a A + b B → c C + d D:

$v=-{\frac {1}{a}}\cdot {\frac {d[A]}{dt}}=-{\frac {1}{b}}\cdot {\frac {d[B]}{dt}}={\frac {1}{c}}\cdot {\frac {d[C]}{dt}}=-{\frac {1}{d}}\cdot {\frac {d[D]}{dt}}$

Let's take a closer look at the relationship between reaction rate and reactant concentration. Consider a simple reaction X → Y. Its rate will be proportional to [X] according to the equation:

(15)

$v=-{\frac {d[X]}{dt}}=k\cdot [X]$

where k is the rate constant.

In some cases, the rate may be proportional to [X]², may depend more complexly on [X], or conversely may not depend on [X] at all (in which case the reaction proceeds at a constant rate). The exact relationship between the reaction rate and the concentration of the reactants is an ``empirical fact and - especially if we consider reactions with more complex reaction mechanisms - cannot be derived only from the stoichiometry of the observed transformation.

Chemists define the ``kinetic order of a reaction by the number of terms whose concentrations affect the rate. If the speed does not depend on the concentration, and therefore the equation v = k applies, we speak of the zeroth order. If the rate is directly proportional to the concentration of one of the reactants, it is first-order kinetics (as in the case of the above-mentioned reaction (15)). If the rate is affected by the concentration of two reactants or if it is an exponential relationship of one reactant (v = k · [X] · [Y] or v = k · [X]²), we speak of second-order kinetics etc.

Sometimes we want to predict how much reactant X will remain unreacted after a time t from the start of the reaction, or how long it will take for [X] to halve. For zero-order reactions, the calculation is simple, but for higher orders it gets complicated.

For a first-order reaction:

(16)

$-{\frac {d[X]}{dt}}=k\cdot [X]$

Integrating equation (16) we get:

$-{\frac {1}{[X]}}\cdot {\frac {d[X]}{dt}}=k\cdot [X]$

$-\int {{\frac {1}{[X]}}\cdot {\frac {d[X]}{dt}}}=\int {k\cdot [X]}$

(17)

$-ln[X]=k\cdot t+c$

By solving for the beginning of the reaction, i.e. for t = 0 (while we denote the initial concentration of substance X at this time as [X]₀), we get

(18)

$c=-ln[X]_{0}$

$-ln[X]=k\cdot t-ln[X]_{0}$

$-ln[X]+ln[X]_{0}=k\cdot t$

$-ln{\frac {[X]}{[X]_{0}}}=k\cdot t$

${\frac {[X]}{[X]_{0}}}=e^{-k\cdot t}$

(19)

$[X]=[X]_{0}\cdot e^{-k\cdot t}$

This equation describes the exponential decay of X concentration over time. A useful parameter of exponential decay is the time required to reduce the initial concentration (or amount) of substance X by half. It is called the half-time'' (t_1/2). From equation (19), we can express the half-time as:

$t_{1/2}={\frac {ln2}{k}}$

Fontana J., Trnka J., Maďa P., Ivák P. et al.: Transformation of substances and energy in the cell. In: Functions of cells and the human body : Multimedia scripts.