Sound Intensity
|
Check of this article is requested. |
|
This article was marked by its author as Under construction, but the last edit is older than 30 days. If you want to edit this page, please try to contact its author first (you fill find him in the history). Watch the discussion as well. If the author will not continue in work, remove the template Last update: Monday, 08 Dec 2014 at 5.41 pm. |
|
This article was checked by pedagogue, but later was changed. |
Sound Intensity[edit | edit source]
Introduction[edit | edit source]
Sound intensity is the amount of energy per unit (1m2) per unit of time (1s).
Formula of sound intensity[edit | edit source]
The greater the amplitude of the vibrations through a certain medium, the higher the energy of the particles is and thus, the intensity of the sound wave is higher. The formula for sound intensity is: I = E/(A*t). Seeing as E/t is the same as the power (P), we can simplify this formula into I = P/A.
Measuring[edit | edit source]
Another unit for the sound intensity is decibels (dB). This is a logarithmic scale, in which 0 dB the same is as the threshold of hearing with an intensity of 1*10-12 W/m2. For every 10 decibels that the sound intensity is increased by, the intensity goes up by a power of 10. So if the sound intensity level is increased from 0 to 20 decibels, the intensity is increased by 10*10=100, meaning that the sound intensity is 1*10-10 W/m2. The formula for this relationship is: dB = 10*log(I/I0). Here I0 is the threshold of hearing and I is the sound intensity.
Distance[edit | edit source]
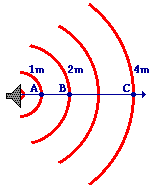
The further away from a sound source a person is the lower the sound intensity is. The mathematical relationship between the distance and sound intensity is known as an inverse squared relationship. This means that as the distance from a source is doubled, the sound intensity is quartered.
| Distance | Intensity |
|---|---|
| 1 m | 160 units |
| 2 m | 40 units |
| 3 m | 17.8 units |
| 4 m | 10 units |
References[edit | edit source]
http://en.wikipedia.org/wiki/Sound_intensity
http://www.physicsclassroom.com/class/sound/u11l2b.cfm
http://hyperphysics.phy-astr.gsu.edu/hbase/sound/intens.html }}
