Reflection
Upon impact at the interface of two media with different optical properties, the incident light is partially reflected and partially passes through the interface (we say that the light is refracted). We call these optical phenomena reflection and refraction of light.
Refraction and reflection of light[edit | edit source]
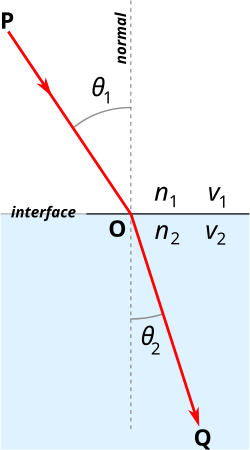
Reflection (reflection) and refraction (refraction) of light are optical phenomena that occur at the interface of two optically different environments in which light propagates at a different phase speed. For these phenomena, we describe: angle of incidence of light (α) = at what angle the light hits the interface, angle of incidence
(α´) and angle of refraction (β). Next, we describe the perpendicular of incidence (normal), which is a line perpendicular to the optical interface at the point where the beam hits.
The angle of reflection is according to the law of reflection equal to the angle of incidence, and the reflected ray lies in the plane determined by the normal and the incident ray.
Refractive index[edit | edit source]
Each environment is characterized by a refractive index (n). We distinguish between absolute and relative index of refraction.
The absolute index of refraction determines how many tomes light propagates more slowly in a given medium than in a vacuum (n = c/v). It follows from the definition that the index of refraction of vacuum is 1 and all other media have a larger index of refraction (n >1).
The relative (n12) refractive index is defined as the ratio of the velocities of light in two optically different media v1 and v2:
Examples of refractive index:
| Substance | Refractive index |
|---|---|
| vacuum | 1 |
| air (normal pressure) | 1,00026 |
| ice | 1,31 |
| water | 1,33 |
| ethanol | 1,36 |
| glycerol | 1,473 |
| glass | 1,5–1,9 |
| salt | 1,52 |
| sapphire | 1,77 |
| diamond | 2,42 |
At the interface of two environments, we distinguish between optically denser (n2) and thinner (n1) environments. Based on this distinction, we determine refraction to the perpendicular and refraction away from the perpendicular.
Snell´s law (Law of Refraction of Light)[edit | edit source]
Snell´s law belongs to the basic laws describing the propagation of waves that pass (so-called refraction) across an interface from one medium to another with a different refractive index. E.g. water - air, glass - air.
It bears the name of one of the discovers, the Dutch mathematician W. van Snell.
The ratio of the sines of the angle of incidence (α) and the angle of refraction (β) is equal to the ratio of the velocities in the given medium and the inverse ratio of refractive indices. According to this law, we distinguish between refraction from the perpendicular and refraction to the perpendicular.
sin α/sin β = v1/v2 = n2/n1
Refraction to the perpendicular occurs when the beam propagates from an optically thinner medium to an optically denser medium (α > β).
Refraction from the perpendicular occurs when the beam propagates from an optically denser medium to an optically thinner medium (α < β).
Refraction and reflection of light go hand in hand. A special case occurs when the refraction angle is equal to 90o. Such an angle of incidence is called the limiting angle (αm). If the angle of incidence is greater than the limiting angle, the so-called total reflectionoccurs. It occurs only in the transition between an optically denser and an optically thinner environment and not the other way around.
Another reflection angle is the Brewster (polarization) angle. A beam reflected at this angle is polarized.
tg αB = n12 = n2/n1
Derivation of Snell´s law[edit | edit source]
We derive Snell´s law from Fermat´s principle.
The wording of Fermat´s principle: Light propagates in space from one point to another along such a path that the time required to cover this path takes on extreme value.
In the vast majority, the extreme is the minimum and this is used in the derivation.
The path traveled by the light from point A to point B and from point B to point C is calculated as the diagonals of the quadrilaterals: s = s1 + s2 = √(y12 + x12) + √(y22 + x22)
Time for light to cover path: t = t1 + t2 = s1/v1 + s2/v2 = √(y12 + x12) / v1 + √(y22 + x22)/v2
Now the minimum of the total time function is calculated. We derive the function (x1) according to the variable x1 and set the result of the derivative equal zero.
1/v1 × x1/√(y12 + x12)
− 1/v2 × x2/√(y22 + x22)/v2 = 0
From the future we can conclude that the sine of an angle in a right triangle is equal to the ratio of the opposite side to the hypotenuse.
sinα = x1/√(y12 + x12)
sinβ = x2/√(y22 + x22)
As we can see, we can substitute both sinα and sinβ into the equation and after adjustment we get the expression:
1/v1 × sinα − 1/v2 × sinβ = 0
After modification we get Snell´s law of refraction:
sinα/sinβ = v1/v2
Links[edit | edit source]
Related Articles[edit | edit source]
References[edit | edit source]
- NAVRÁTIL, Leoš – ROSINA, Jozef, et al. Medicínská biofyzika. 4. edition. 2005. ISBN 978-80-247-1152-2.
- KOLEKTIV AUTORŮ,, et al. Odmaturuj! z fyziky. 2. edition. 2006. ISBN 80-7358-058-6.