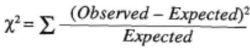Fourfold and Contingency Tables

Chi-squared Test

Contingency tables are used to determine whether 2 distinct variables are linked. To be able to quantify such linkage, we use the chi-squared (χ²) test.

The variables can be:

• Qualitative
• Discrete quantitative
• Continuous quantitative, whose values have been grouped (i.e.: intervals).

When there are two such variables the data are arranged in a contingency table: Variable #1 → rows Variable #2 → columns

Individual members of the sample/population are assigned to the appropriate cell of the contingency table according to their values for the two variables. When the table has only two rows or two columns this is equivalent to the comparison of proportions. In this case it is called four-fold table.

The use of the chi-squared test is not confined to nominal and ordinal data but can also be used for continuous variables that have been categorized. The procedure described for four-fold table can be easily applied for any contingency table.

Example

The medical hypothesis is that progressive polyarthritis (PAP) is associated with the HLA-DR4 antigen. Observed frequencies in the sample of 308 patients divided according to presence of PAP and HLA-DR4:

	HLA-DR4 +	HLA-DR4 -	Total
PAP +	46	28	74
PAP -	50	184	234
Total	96	212	308

Statistical testing is based on reformulating the medical hypothesis in two statistical hypotheses, i.e. null hypothesis H₀ and the alternative hypothesis H₁.For our medical hypothesis the statistical hypotheses are as it follows:

• H₀: There is no association of PAP with HLA-DR4 (always state no association)
• H₁: PAP is associated with HLA-DR4. (the opposite to H₀)

We intend to verify the null hypothesis on 5% significance level using data given in the table above (the observed frequencies). Next, we calculate the expected values for each cell. Generally, the expected frequency in the cell of the i-th row and j-th column can be calculated as the sum of the i-th row multiplied by the sum of the j-th column and divided by the total number of patients.

Table of expected values

	HLA-DR4 +	HLA-DR4 -	Total
PAP +	23	51	74
PAP -	73	161	234
Total	96	212	308

Then, the observed and expected frequencies are compared. If the two variables are associated, the observed and expected frequencies should be close together, any discrepancy being due to random variation. The best way of looking at the differences between observed and expected frequencies is to calculate the chi-squared (χ²) statistic as follows:

where the summation includes all the cells in the table. For the above example the test statistic is χ² = 43.61

In order to interpret this chi-squared statistic, we need to know the number of degrees of freedom(df) involved For a contingency table this is given in general by the formula df = ( number of rows - 1) x (number of columns - 1). In the above example there are 2 rows and 2 columns so we have df = (2-1)*(2- 1) = 1 Referring to the table which shows the percentage points of the χ² distribution, we can see the value of 43.61 is greater than 3.84 the critical value for 95% level of significance (p value=0.05).

In general:

• If the calculated χ² > critical value → reject H₀ hypothesis and accept H₁
• If the calculated χ² < critical value → do not reject H₀

In our example, we reject the null hypothesis, meaning: there is association between PAP and HLA-DR4 and this conclusion has less than 5% probability that there could be huge differences in the observed values arising just by chance.

Links

Related articles

• Hypothesis Testing

Bibliography

• BENCKO CHARLES UNIVERSITY, PRAGUE 2004, 270 P, V, et al. Hygiene and epidemiology. Selected Chapters. 2nd edition. Prague. 2008. ISBN 9788024607931.