Bernoulli equation
|
Check of this article is requested. Suggested reviewer: Carmeljcaruana |
Bernoulli’s equation
The Bernoulli’s equation shows how the pressure and velocity vary from one point to another within a flowing fluid. It says that the total mechanical energy of the fluid is conserved as it travels from one point to another, but some of this energy can be converted from kinetic to potential energy and its reverse as the fluid flows. In fluid dynamics, which is the study of fluid motion and its associated external forces and internal resistances, the Bernoulli’s equation relates pressure to energy. Bernoulli’s equation states that in an ideal fluid, when the flow is uniform and continuous, the sum of the pressure, kinetic energy, and potential energy of a fluid is constant.
How does it work?
The Bernoulli’s principle states that the sum of PRESSURE AND the POTENTIAL energy and the kinetic energy of a fluid PER UNIT VOLUME flowing through a tube is constant. A greater energy associated with pressure in the fluid corresponds to lower KINETIC AND POTENTIAL energy. The decrease in pressure when the fluid velocity increases (AND VICE VERSA) is called the Bernoulli effect .
So, the Bernoulli’s equation states:
===== P₁ + ½𝜌v₁² + 𝜌gh₁ = P₂ + ½𝜌v₂² + 𝜌gh₂ =====
P₁= pressure at point 1
½𝜌v₁² = Kinetic energy PER UNIT VOLUME at point 1
𝜌gh₁ = Potential energy PER UNIT VOLUME at point 1
P₂ = pressure at point 2
½𝜌v₂² = Kinetic energy PER UNIT VOLUME at point 2
𝜌gh₂ = Potential energy PER UNIT VOLUME at point 2
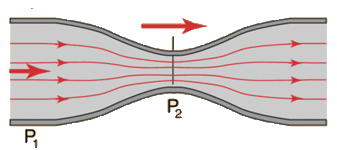
This diagram on the right shows a blood vessel that is narrowed and returning to its normal diameter. In the narrowed area(obstruction of flow) as the diameter decreases, the velocity increases (BY THE CONTINUITY EQUATION). If the diameter is reduced by half, the velocity is increased by 4, making kinetic energy increase accordingly. Assuming that the energy is conserved, the increase in kinetic energy PER UNIT VOLUME results in the decrease IN PRESSURE. When the vessel returns to its original diameter, the kinetic energy will also return back to its original value, AND SO DOES THE PRESSURE.
One disadvantage of the Bernoulli’s equation is that it can be complicated for routine clinical use, however, a simplified version (𝝙P=4v² ? NEEDS REFERENCE
) tells us the difference in pressure between the right ventricle and the right atrium, given that there is no heart valve disorder.
Importance in clinical medicine
In echocardiography, the Bernoulli’s principle can be applied when interpreting blood flow, which can describe a decrease in localized pressure produced by high flow rate near blockages as mentioned above with an illustration. For clinical medicine, the simplified equation allows for an easy estimation of pressure gradients from velocity.
Another use of Bernoulli's equation is with the venturi mask. The venturi mask is a medical oxygen mask that delivers a concentration of oxygen to patients on controlled oxygen therapy. There is a tube from the mask that is connected to a nozzle which connects to a supply of pure oxygen(usually from the hospital wall). The tube, that is directly connected to the mask has a small window which allows room air(oxygen poor) to flow into the mask. The venturi mask can control the amount of oxygen poor air( the air that we normally breathe) that flows in, along with pure oxygen delivered from its connected nozzle. As oxygen flows into the tube, it creates a decrease in pressure due to oxygen passing through a narrow opening of the tube. This drop in pressure allows air to flow into the mask, mixing with the pure oxygen from the nozzle, which is the consequence of Bernoulli's principle.
Who is the father of the Bernoulli's equation?
The Bernoulli’s equation was derived by Daniel Bernoulli(1700-1783) in the 1730s. Daniel Bernoulli was a Swiss mathematician and physicist born into a family of mathematicians, including his father, Johann Bernoulli, and his uncle, Jacob Bernoulli.
He published a book called Hydrodynamica(1738) where he explained fluid mechanics, with the idea of conservation of energy in mind, and hydrodynamics. The book describes the nature of hydrodynamic pressure in fluid flow which later became to be known as the Bernoulli’s principle.
He was greatly honored during his lifetime and still is held in high respect in the field of mathematical physics. [[File:]]
References:
Giordano, Nicholas; College Physics: Reasoning and Relationships; 2nd Ed.; 2013; 978-0-8400-5819-5
Rama, Durhaiah D.; Fluid Mechanics and Machinery; 1st Ed.; 2002; 81-224-1386-2
Griffin Brian P.; Manual of Cardiovascular medicine; 4th Ed.; 2013; 978-1-4511-3160-4
Klabunde Richard E.; http://www.cvphysiology.com/Hemodynamics/H012.htm
Anesthesia UK; http://www.frca.co.uk/article.aspx?articleid=100482