Distribution function

A distribution function , sometimes referred to as a cumulative probability distribution (from the English cumulative distribution function ), is a function according to which the probability distribution of a random variable can be unambiguously described . At the same time, it is a function where the value of the random variable is always smaller than the specified value, i.e. the numerical realization of the random variable (usually referred to as) does not exceed the specified value on the given real axis x.

Description and formulas

We denote the distribution function $F(x)$, whereas:

An illustrative example of the distribution function in several cases with different values ​​of the mean and variance of the normal distribution . The standardized normal distribution is indicated by the red function.

Failed to parse (syntax error): {\displaystyle F(x)=\mathrm{P}(X \le x) = P(ω_i \in Ω : X (ω_i)\le x)}

Rozdělení	Distribuční funkce
[[Uniform distribution]] on the interval $[\alpha ,\beta ]$	$F(x)=\left\{{\begin{array}{ll}0&x<\alpha \\{\frac {x-\alpha }{\beta -\alpha }}&x\in [\alpha ,\beta ]\\1&x>\beta \end{array}}\right.$
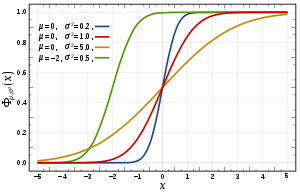
Normal distribution	$F(x)={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}\int \limits _{-\infty }^{x}\exp \left\{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right\}$
Exponential distribution	$F(x)=\left\{{\begin{array}{ll}0&x<0\\1-\exp\{-\lambda x\}&x\geq 0\end{array}}\right.$

Properties

Since the distribution function is defined as a probability, we assign it several basic characteristics:

1. it is a non-decreasing function $\alpha <\beta \Rightarrow F(\alpha )\leq F(\beta )$;
2. continuous right $\lim _{x\to \alpha ^{+}}F(x)=F(\alpha )$;
3. its asymptotic properties say that it is defined in the interval from zero to one inclusive $\lim _{x\to +\infty }F(x)=1$ a $\lim _{x\to -\infty }F(x)=0$.

At the same time, it is worth mentioning that this is a function inverse to the quantile function, in which the result is not a probability (as in the case of a distribution function), but a number on the real axis that corresponds to the investigated probability. It therefore holds that:

Distribution function: $F(x_{p})=\mathrm {P} (X\leq x_{p})=p$

Quantile function: $x_{p}={F^{-1}}\mathrm {P} (X\leq x_{p})={F^{-1}}(p)$

Links

related articles

• Normal distribution
• Poisson distribution
• Student's distribution
• Measures of variability
• Position measures

References

• WOOLSON, Robert F. – CLARKE, William. Statistical Methods for the Analysis of Biomedical Data. 2. edition. John Wiley & Sons. Inc., 2002. 368 pp. ISBN 9780471394051.